VFiasco Project FAQ

Questions answered in this FAQ

• What is a µ-kernel?
• What does a µ-kernel-based system look like?
• I have more µ-kernel-related questions or questions about Fiasco.

• Do you need a programming language with completely defined semantics?
• Do you assume a virtual machine that runs Safe-C++ programs?

• How do you find out which operating-system properties are worth verifying?
• The hardware model and the translated kernel source code you load into the theorem prover have direct counterparts in the real world. What is the counterpart of the object-store layer?
• Don't you also have to verify the the C++ compiler with which you compile Fiasco?

• Why do you use a coalgebraic specification language (CCSL)? Why don't you just specify your interfaces with properties in a theorem prover and verify your models adhere to them?
• What is a final model good for? When would I use it as opposed to using a specific model (translated source code) or using the specification?
• During verification, when would I use a specification, a specific model (translated source code), a final model, or an arbitrary model?

Questions and Answers

What is a µ-kernel?

A µ-kernel, or microkernel, is an operating system kernel which provides only essential services such as tasks, threads, inter-process communication (IPC), and memory management primitives. All servers -- including device drivers -- run in user mode and are treated by the µ-kernel just like any other application. Since each server runs in its own address space, all these objects are protected from each other.

This design has a number of sofware-technological advantages:

• Servers for different APIs, file systems, and even different operating system personalities can coexist in one system.
• The system is very flexible. For a given application, only selected servers need to be added to the system. Modified servers can be tested online; they do not require building or booting a new kernel and do not affect the running system.
• Server or device driver malfunction is isolated to the tasks they are running in.
• Interdependencies between the servers of a system can be restricted so that the trusted computing base for security-critical applications can be reduced.
• The mechanisms provided by the µ-kernel (IPC, multithreading) can be used by all servers and applications.
• A clean µ-kernel interface enforces a more modular system structure.

Please also see the answer to the next question. (hohmuth 98/10/07)

What does a µ-kernel-based system look like?

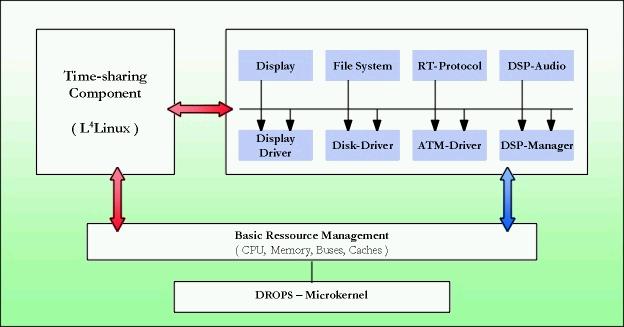
The DROPS project is an example for a µ-kernel-based system.

In DROPS, real-time (multimedia) and time-sharing components coexist on one system. In DROPS, a port of the Linux kernel to L4, L⁴Linux, provides a standard time-sharing API; it is binary-compatible to Linux (i.e., it runs unmodified Linux binaries). L⁴Linux not only runs on L4/x86, but also on Fiasco.

Real-time applications use servers which are independent from L⁴Linux. However, L⁴Linux applications can use these servers, too, in time-sharing mode via stub drivers in the L⁴Linux server.

DROPS uses the Fiasco microkernel as its implementation of L4. (hohmuth 98/10/07)

What is new in the Fiasco µ-kernel?

Fiasco is the first L4-compatible kernel which supports real-time applications: The kernel is preemptible at virtually any time, guaranteeing low activation latencies for threads with high priorities. Because it is constructed around non-blocking synchronization strategies, in-kernel deadlocks and priority inversion are prevented while at the same time programming the kernel becomes easier.

Other than that, Fiasco is just another implementation of the L4 µ-kernel interface. It is a second-generation µ-kernel, faithfully following the L4 design principles: Improving performance by careful kernel design, and providing only mechanisms for application writers, but not imposing mandatory policies. (hohmuth 98/10/07)

I have more µ-kernel-related questions or questions about Fiasco.

Please visit the Fiasco website, in particular the Fiasco FAQ. You can also ask microkernel-related questions on our mailing list <l4-hackers@os.inf.tu-dresden.de>. (hohmuth 2001/11/15)

Do you need a programming language with completely defined semantics?

Part of the verification is to prove that the kernel uses only well-defined programming-language constructs. This includes avoiding constructs that are undefined in C++, such as dereferencing a pointer after free has been called on it. So, technically, many constructs that invoke undefined behavior in standard C++ can remain undefined in Safe C++.

That said, however, Safe C++ will contain some definitions for previously undefined behavior, and restrictions of previously allowed uses, for two reasons. First, restricting what is allowed in Safe C++ (such as restricting copying of pointers to automatic variables) eases verifying the software. Second, defining more behavior (such as dereferencing dangling pointers) helps debugging, which always precedes verification because of its lower cost. (hohmuth 2001/11/22)

Do you assume a virtual machine that runs Safe-C++ programs?

No. Safe-C++ programs run on the bare hardware, and we also model bare hardware (physical and virtual memory) in the theorem prover. Type and memory safety -- properties we need for comfortable program verification -- must be guaranteed by the Fiasco kernel itself, and proving that Fiasco always provides these guarantees (which we call ``object-store properties'') will be a major part of our verification.

(Our logic compiler translates Safe-C++ source code into its semantics. The output uses formal models of Safe C++'s semantics that are based on object-store properties and our hardware model. These models comprise the equivalent of a Safe-C++ ``virtual machine'' that ``runs'' within the theorem prover. However, this virtual machine models execution on real hardware.)

Please refer to our technical report for more information.

How do you find out which operating-system properties are worth verifying?

First and foremost, we will verify that the system does not crash or use undefined features of C++. This property becomes an automatic proof obligation based on the C++ semantics we use (see our technical report, Section 3 [A semantics of C++]).

Second, we will verify that each module fulfills its specification, that is, that it works correctly. In a first step, we will only include in these specifications properties that we need for proving system safety.

Third, we verify some security properties for the whole kernel. Deciding on which properties to verify is nontrivial. While everybody can quickly come up with a wish list of items like separate address spaces, authenticated IPC, or support of secure installation and booting, up to now nobody seems to have come up with a list of formal security properties that are worth verifying. We have several ideas for generating such a list:

1. Trivial pursuit. All of us can think of properties which are obviously required for a safe operating system, such as address-space protection, kernel-memory protection, trusted software-installation process, and so on.

   This approach would require thinking of more such obvious properties (or squeezing them out of experts such as implementors of secure applications), and finding a rationale for them.

2. Examine a subject. Look at one or two specific applications that need security guarantees from the system, for example the Anonymous-web-surfing proxy, the Perseus system or the DROPS console subsystem (DROPS is an operating system that runs on top of L4/Fiasco). Assume an attacker model in which the attacker can execute arbitrary code (such as Trojan horses) on the system. What guarantees does the application require from the operating system in order to be able to guarantee its own security goals?

3. Bug hunt. Classify known attacks (such as those described by CERT) based on attacker model and violated security goal. Filter out attacks on operating systems or system software. Think of countermeasures that could have prevented the remaining classes of attacks (e.g., better access control, stack not executable).

4. Access-control breakdown. As one representative class of OS-level security mechanisms, look at access-control mechanisms such as access-control lists, mandatory access control, BSD jails, virtual machines, and other sand-boxing mechanisms. Derive security properties these mechanisms provide, and break these down to requirements on the microkernel.

5. The rules of the game. Analyze a security calculus. There exist calculi (similar to process calculi) that allow reasoning about security protocols. Examples are the BAN logic [Anderson: Security Engineering, page 29], the spi calculus (search the web, for instance [ResearchIndex results]), and maybe also the calculus of mobile ambients [ResearchIndex results]. In these calculi one can prove the correctness of security protocols. The derivation rules of these calculi present the assumption of the calculus about the environment and/or the underlying system. One can now analyze these rules to find a set of properties that guarantee the correctness of the rules. Any system that fulfills these properties is a model for the calculus and thus preserves the truth of all proofs done in the calculus.

6. Question the truth. Analyze a security proof. Take a description of a security protocol and an explanation why it is secure. For instance the RSA key exchange protocol, or the SSH protocol. Examine the explanation for basic operations such as "send a message", "decipher", "read key" ... Consider these basic operations as operating system primitives. Design a set of properties of this hypothetical system that are necessary assumptions of the explanation of the protocol.

(hohmuth/tews 2002/05/28)

The hardware model and the translated kernel source code you load into the theorem prover have direct counterparts in the real world. What is the counterpart of the object-store layer?

The object-store layer provides a set of high-level interfaces for allocating and manipulating typed objects, with proofs about the type safety of its operations. It is based on the low-level hardware model, which mainly consists of a byte store. The proofs use preconditions that must be ensured by Fiasco itself; for example, Fiasco must not overwrite (using byte-level operations) memory regions in which typed objects are stored. Proving these preconditions will be a major part of the VFiasco project.

Therefore, the object-store layer encapsulates knowledge about the Safe-C++ type system implemented in the Safe-C++ compiler. (hohmuth 2002/06/10)

Don't you also have to verify the the C++ compiler with which you compile Fiasco?

Yes -- just as we have to verify the logic compiler, the theorem prover, the operating system and hardware platform on which we run the verification, and the hardware on which Fiasco runs.

Seriously, the world will not be perfect when we have verified Fiasco. Still, we will significantly increase the trust that can be put into a Fiasco-based system, which in itself is a big step forward. (hohmuth 2002/06/10)

Why do you use a coalgebraic specification language (CCSL)? Why don't you just specify your interfaces with properties in a theorem prover and verify your models adhere to them?

In fact, most module-interface or class-interface specifications already are coalgebraic in nature and can be expressed directly in higher-order logics. Using CCSL to compile specifications has the advantage of making it possible to automatically generate definitions useful during verification:

Notion of bisimulation.

CCSL provides a definition of bisimulation (equivalence of behavior), which is a weaker but more useful relation than strict equality.

Notion of final model, coinduction.

CCSL provides definitions for a specification's final model (sometimes also called terminal model; the type of all states that behave differently; i.e., the type of all states of all models that fulfill the specification, modulo bisimulation). This model enables a powerful new proof method, coinduction. See also the next FAQ entry.

Modal operators.

Modal operators allow to succinctly express safety and liveness properties. CCSL generates these operators and appropriate lemmas for all specified classes and enables proofs that require knowledge of all reachable states from a known initial state.

(hohmuth 2001/11/15)

What is a final model good for? When would I use it as opposed to using a specific model (translated source code) or using the specification?

The final model of a specification contains all possible behaviors that a specification might exhibit. When we have proven that a given model is the final model, we can make use of it mainly in four ways:

Consistency

Once we have constructed a final model, we can be sure that the specification is not inconsistent and that there actually exists a model for the specification.

Accuracy

We can use it to verify that the specification accurately encodes the intended behavior.

Simplicity

We can use it to ensure that the specification's interface is a simple and efficient way of encoding the intended behavior, and that it does not allow for unintended or extra behavior.

Coinduction

The final model of some specification A can help verify another model M that uses A's interface, or proving theorems concerning A, by enabling a powerful proof method, coinduction. Coinduction is the coalgebraic equivalent of induction on algebraic data types (such as natural numbers or lists).

(hohmuth 2001/11/22)

During verification, when would I use a specification, a specific model (translated source code), a final model, or an arbitrary model?

A specification would generally be used to describe the interface and the behavior of a software module.

A specific model of some specification would normally only be used during verification of that model. Verification normally consists of proving that the model fulfills the specification and exposes no unwanted behavior.

The final model can be used in various ways (see previous FAQ entry). It becomes important if one uses specifications to create new types. For instance, if one creates a specification of infinite sequences and constructs (via the final model) the type of all infinite sequences from that specification, then one would probably use coinduction to reason about elements of this new type.

In verifying software that is based on the design-by-contract model the final model of a specification is rarely needed (except for meta-theoretic reasoning described in the previous FAQ entry).

An arbitrary model is a model that is assumed to fulfill a given specification A. We assume an arbitrary model of A when we verify client models that use A's interface. (hohmuth 2001/11/22)